1 背景介绍

1.1 研究背景

随着集成电路技术的迅猛发展，特别是纳米级工艺的实现，跨导运算放大器朝着高增益、高带宽以及低功耗的方向发展，其信号处理的能力也在不断的提高。但是目前 OTA 仍然是制约模拟电路 IC 设计的一个瓶颈。作为模拟电路的一个基本单元，OTA 电路需要具有一个较宽的带宽和一个较高的直流增益。但是在实际的电路设计中，这两个指标通常是相互矛盾的，并且被有限的跨导、较小的输出电阻以及较低的偏置电压限制。

在实际的电路设计中，为了获得一个较高的增益，在对运放进行设计时通常会采用两级级联的结构，通过将两级的运放增益进行叠加从而获得增益的提升。但是直接叠加的两级运放会存在稳定性的问题。因此，为了在能够保证运放增益的前提下提升运放的稳定性，通常需要对两级运放进行补偿。

1.2 常规的 OTA 补偿方案

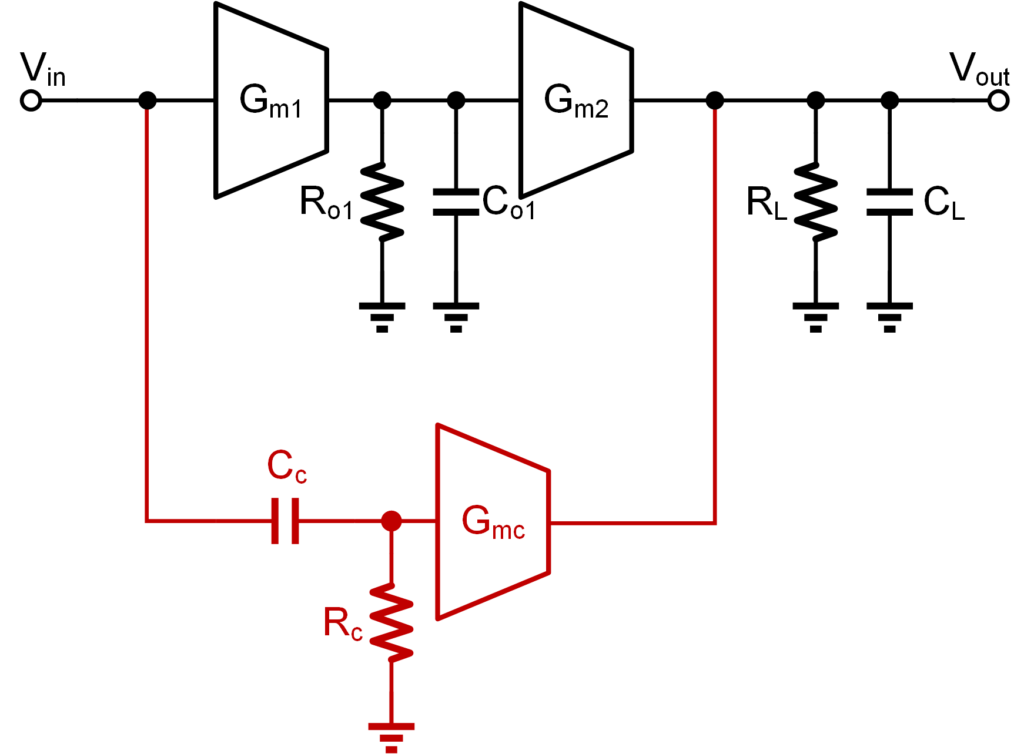
常规的 OTA 补偿通常使用密勒补偿的方式进行，其电路结构如图1-1所示。密勒补偿主要是通过在第二级运放的输入端和输出端之间并联一个较大的密勒补偿电阻从而实现对电路的稳定性补偿。

密勒补偿的原理是基于密勒效应进行的。密勒效应效应（Miller effect）是在电子学中的一种效应，表现在对于反相放大电路中，输入与输出之间的分布电容或寄生电容由于放大器的放大作用，其等效到输入端的电容值会扩大1+K倍，其中K是该级放大电路电压放大倍数。通过利用密勒效应，就可以在第一级放大器的输出端引入一个较大的负载电容，进而将运放的主极点和次级点分离开来，从而达到对运放的相位裕度进行补偿的效果。

2 密勒补偿型运放存在的问题

密勒补偿运放作为一个目前最常用的补偿结构，它在高带宽应用下会体现出一定的功耗问题，下面将对该问题进行分析。

2.1 密勒补偿型运放的零极点

对于图 1-1 中所示的密勒补偿型运放，可以推导出它输入到输出的传递函数为：

$$ H(s)=\frac{G_{m1}G_{m2}R_{o1}R_L(1-sC_c/G_{m2})}{P(s)} $$

其中：

$$ \begin{aligned} P(s) = & 1+s[R_{o1}(C_{o1}+C_c)+R_L(C_L+C_c)+G_{m2}R_{o1}R_LC_c] \\ & +\,\,s^2R_{o1}R_L(C_{o1}C_L+C_cC_{o1}+C_cC_L) \end{aligned} $$

通过该表达式可以看出，该运放的低频增益可以表示为：

$$ A=G_{m1}G_{m2}R_{o1}R_L $$

该运放的主极点和次级点分别可以表示为：

$$ \begin{aligned} \omega _1 & =\frac{1}{R_{o1}[C_{o1}+(1+A_{v2})C_c]}=\frac{1}{G_{m2}C_cR_{o1}R_L} \\ \omega _2 & =\frac{G_{m2}C_c}{C_{o1}C_L+C_cC_{o1}+C_cC_L}=\frac{G_{m2}}{C_L} \end{aligned} $$

将增益表达式和运放的主极点表达式相乘，即可求出运放的增益带宽积表达式为：

$$ GBW=\frac{G_{m1}}{C_c} $$

可以看出，该运放的增益带宽积与第一级运放的跨导和密勒补偿电容的电容值直接相关。

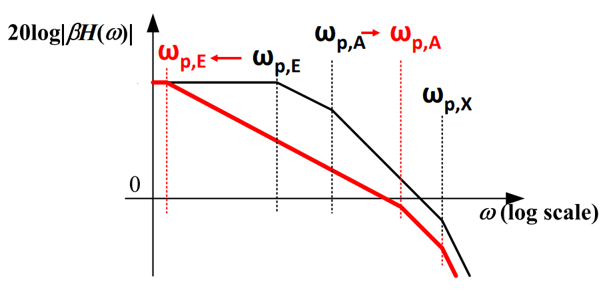
对于，密勒补偿型两级运放，其幅频特性曲线曲线如图2-1所示，可以看出添加的密勒补偿电容实现了两个极点的分离，进而完成了补偿。

2.2 密勒补偿的运放存在的问题

通过上述推导可以得出，两级密勒补偿运放的 GBW 和次级点的表达式为：

$$ GBW=\frac{G_{m1}}{C_c}, \omega _2=\frac{G_{m2}}{C_L} $$

然而，一个运放的相位裕度和该运放的增益带宽积以及次级点的位置具有一个非常紧密的关系。对于一个通常的两级密勒补偿型运放，假设如果最终需要达到 45 度的相位裕度，那么在对该运放进行设计时，需要要求它的次级点位置大于 1.22 倍 GBW；如果最终要求 60 度的相位裕度，则需要要求它的次级点位置大于 2.2 倍 GBW；而如果要求 72 度的相位裕度，那么在进行运放设计时就需要要求它的次级点位置大于 3 倍 GBW。

在通常的电路设计中，会希望运放具有一个较好的相位裕度，从而获得一个较好的稳定性。在这种情况下，对于一个高带宽的应用，在对运放进行设计时，将不仅仅需要通过使用一个较高的功耗来增大第一级运放的跨导，从而实现一个较高的带宽；同时为了保证相位裕度，还需要一个较大的功耗来增大第二级的跨导，进而将整个运放的次级点推到一个更远处，从而实现一个较好的相位裕度。如果运放的输出负载较高，则运放第二级的功耗将会非常大，从而造成严重的功耗消耗。

3 Gm 前馈补偿两级运放

为了解决上述密勒补偿运放存在的问题，人们提出了 Gm 前馈补偿两级运放，来对两级运放进行稳定性补偿。下面本文将对该运放的传递函数进行推导，并将其与密勒补偿型运放进行一个对比。

3.1 传递函数推导

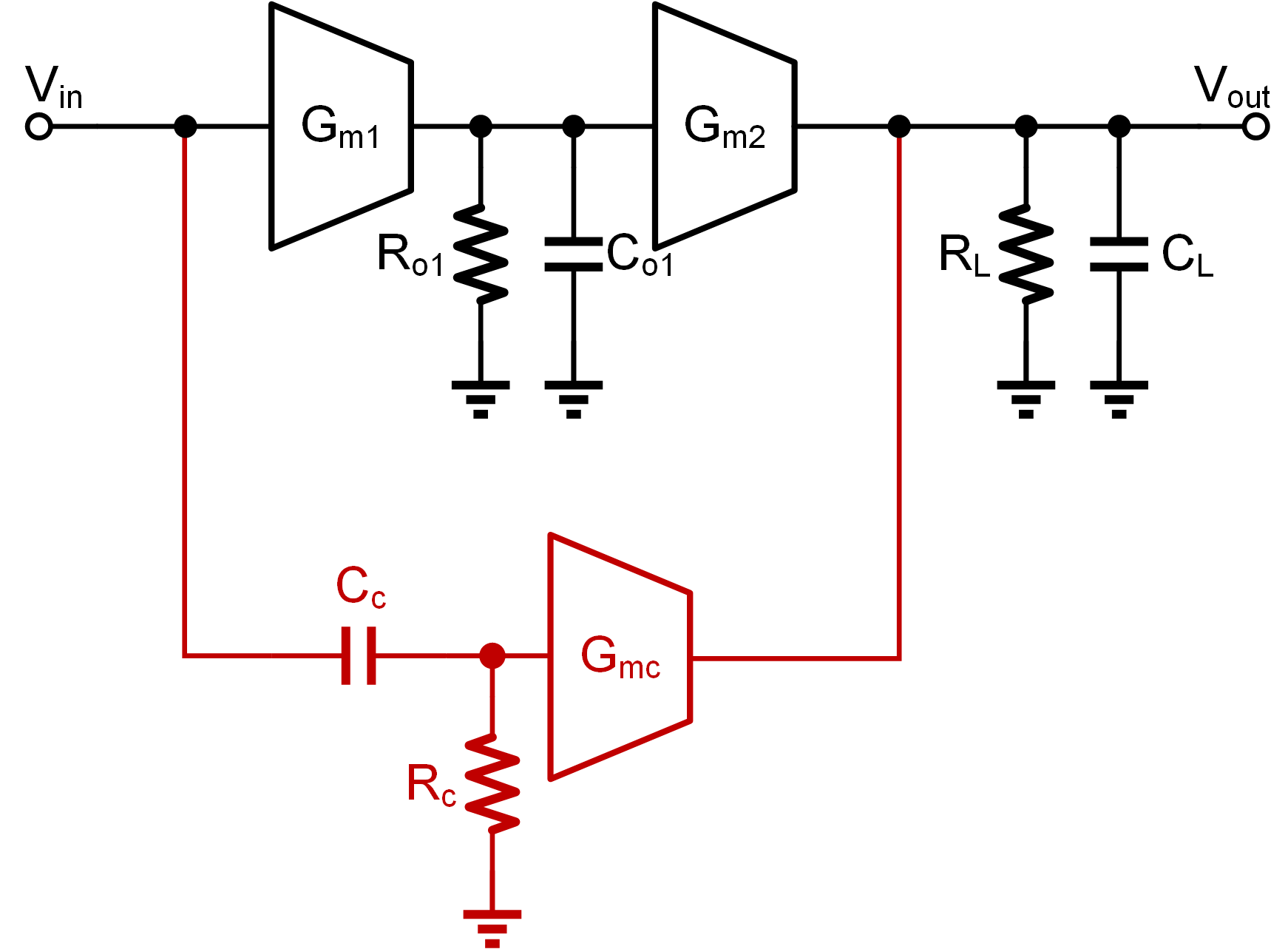
通常的 Gm 前馈补偿型运放的系统可以表示为如图 3-1 所示的结构。该运放通过引入一个 Gm 前馈通路，进而对频率特性进行补偿。

通过对该系统结构框图进行数学上推导，可以得出它的输出和输入之间的传递函数表达式为：

$$ \begin{aligned} H(s) & =\frac{G_{m1}G_{m2}R_{o2}R_L}{(1+\frac{s}{\omega _{p1}})(1+\frac{s}{\omega _{p2}})}+\frac{\frac{s}{\omega _c}}{1+\frac{s}{\omega _c}}\frac{G_{mc}R_L}{1+\frac{s}{\omega _{p2}}} \\ & =\frac{G_{m1}G_{m2}R_{o2}R_L+\frac{s}{\omega _c}(G_{m1}G_{m2}R_{o2}R_L+G_{mc}R_L)+\frac{s^2}{\omega _c\omega _{p1}}G_{mc}R_L}{(1+\frac{s}{\omega _{p1}})(1+\frac{s}{\omega _{p2}})(1+\frac{s}{\omega _c})} \end{aligned} $$

式中：

$$ \omega _{p1}=\frac{1}{R_{o1}C_{o1}}, \omega _{p2}=\frac{1}{R_LC_L}, \omega _c=\frac{1}{R_cC_c} $$

可以看出，该传递函数的表达式较为复杂，在实际应用中需要对其进行化简，从而对运放的设计进行指导。

在实际设计中，通常会将 $R_c$ 和 $C_c$ 取为一个较大的数值，因此该电路的传递函数中，分子上的两个零点位置通常会相聚较远。由于分子为一个二阶特性表达式，因此可以通过两根之和公式求出第一个零点位置为：

$$ \omega _{z1}+\omega _{z2}\approx \omega _{z2}=G_{m1}R_{o1}\frac{G_{m2}}{G_{mc}}\omega _{p1} $$

在求出第一个零点后，第二个零点的位置就可以通过两根之积公式求出：

$$ \omega _{z1}=\frac{\omega _{z1}\omega _{z2}}{\omega _{z2}}\approx \omega _c $$

通过上述推导过程可以看出，对于前馈补偿型运放，其低频零点 $\omega_{z1}$ 会与 $\omega_{c}$ 自然抵消，因此在实际设计中只需要调整 $\omega_{z2}$，使得其与 $\omega_{p1}$ 或者 $\omega_{p2}$ 抵消，即可完成对该运放的补偿。此时，该运放将只存在一个极点，变为一个单极点系统，由此对两级运放的稳定性进行补偿。

3.2 前馈补偿方式优势分析

首先先对前面提到的两种运放的零极点和 GBW 表达式进行一个简单的总结。对于密勒补偿型运放，其主极点、次级点和增益带宽积的表达式为：

$$ \omega _1=\frac{1}{G_{m2}C_cR_{o1}R_L}, \omega _2=\frac{G_{m2}}{C_L}, GBW=\frac{G_{m1}}{C_c} $$

而对于 Gm 前馈补偿型运放，其主极点、次级点、前馈补偿零点和增益带宽积的表达式为：

$$ \omega _{p1}=\frac{1}{R_{o1}C_{o1}}, \omega _{p2}=\frac{1}{R_LC_L}, \omega _{z2}=G_{m1}R_{o1}\frac{G_{m2}}{G_{mc}}\omega _{p1}, GBW\approx \frac{G_{m1}}{C_L} $$

通常，集成运放为核心的电路会在系统中作为放大器或者缓冲器，此时该电路的后级通常会连接着一个较大的电容负载，例如后级 ADC 电路的采样电容或者 ESD 电路和 PAD 的寄生等等。在这些电容的影响下，运放的输出端的负载$C_L$通常会大于运放第一级处的负载电容$C_{o1}$。

此时，对于一个没有任何补偿的两级运放，运放输出端的极点$\omega _{p2}=\frac{1}{R_LC_L}$通常会称为该无补偿运放的低频极点（即主极点），而运放输入端的极点$\omega_{p1}=\frac{1}{R_{o1}C_{o1}}$会成为高频极点（即次级点）。

对于密勒补偿，假设在设计时取补偿电容 $C_c = C_L$，则对于密勒补偿结构运放，它的 GBW 表达式变为 $GBW=\frac{G_{m1}}{C_L}$，而次级点表达式为 $\omega_2=\frac{G_{m2}}{C_L}$。假设设计时为了保证运放具有 72 度的相位裕度，则需要次级点位置大于 3 倍的 GBW，由此可以推导出 $G_{m2}$ 与 $G_{m1}$ 的关系为：

$$ \frac{G_{m2}}{C_L} > 3 * \frac{G_{m1}}{C_L}, G_{m2} > 3 * G_{m1} $$

由此可以看出，对于米勒补偿型运放，为了保证相位裕度需要一个较大的功耗来增大第二级的跨导，进而将整个运放的次级点推到一个更远处，从而实现一个较好的相位裕度。

而对于前馈补偿型运放，则其可以通过使用零点补偿的方式补偿掉运放的次级点，只保留运放的主极点，从而将整个放大器变为一个单极点的系统。通常补偿时会选择对运放的次级点 $\omega_{p1}=\frac{1}{R_{o1}C_{o1}}$ 进行补偿，则此时有：

$$ \omega _{z2} = \omega _{p1}, G_{m1}R_{o1}\frac{G_{m2}}{G_{mc}}\omega _{p1} = \omega _{p1} $$

由此可以推导出：

$$ G_{mc} \approx G_{m1}R_{o1}G_{m2} $$

由此，则可以计算出运放 GBW 为：

$$ GBW = \frac{G_{m1}R_{o1}G_{m2}R_L}{R_LC_L} = \frac{G_{m1}R_{o1}G_{m2}}{C_L} \approx \frac{G_{mc}}{C_L} $$

由此可以看出，前馈补偿型运放的 GBW 与 $G_{m1}$ 无关，而正比于运放的 $G_{mc}$。为了得到一个较好的补偿效果，设计时 $G_{mc}$ 需要比 $G_{m1}$ 大 $G_{m2}R_{o1}$ 倍，这个数字通常大于 10。由此，相比于密勒补偿结构运放的 $GBW=\frac{G_{m1}}{C_c}$，前馈补偿运放的 $GBW = \frac{G_{mc}}{C_L}$能够具有一个更大的增益带宽积特性。

换句话说，密勒补偿型运放的 GBW 和功耗的关系是折中的：大的 GBW 需要大的 $G_{m1}$（$GBW=\frac{G_{m1}}{C_c}$），而为了保证稳定性从而需要大的 $G_{m2}$（$\frac{G_{m2}}{C_L} > 3 * \frac{G_{m1}}{C_c}$），进而会产生大的功耗。而前馈补偿型运放中 $G_{mc}$ 的存在打破了这一种折中关系。对于前馈补偿型运放，一个大的 GBW 需要一个大的 $G_{mc}$（$GBW = \frac{G_{mc}}{C_L}$），而稳定性补偿同样要求一个大的 $G_{mc}$（$G_{mc} \approx G_{m1}R_{o1}G_{m2}$），因此两者之间的关系是趋同的，故前馈补偿型运放能够在得到一个大的 GBW 的同时保证一个较好的稳定性。

综上，通过前馈环路的零极点抵消补偿，前馈运放相当于一个单极点放大器。相比于密勒补偿运放，前馈补偿运放的单位增益带宽可以实现 3~5 倍的提高；相比于单级放大器，两级密勒补偿运放的低频增益可以实现 20dB 的提高。如果在单位增益带宽和负载$C_L$确定的情况下，密勒补偿型放大器的$G_{m2}$通常大于前馈零点补偿放大器中的$G_{mc}$，因此功耗将会远大于前馈零点补偿放大器。

4 常用电路结构调研

由于前馈补偿型运放具有高带宽、低功耗的特点，因此被广泛应用于接收机和ADC等需要高速运放的场合，同时也引申出了各种各样的结构，下面将展示一些目前已经被应用的电路结构。

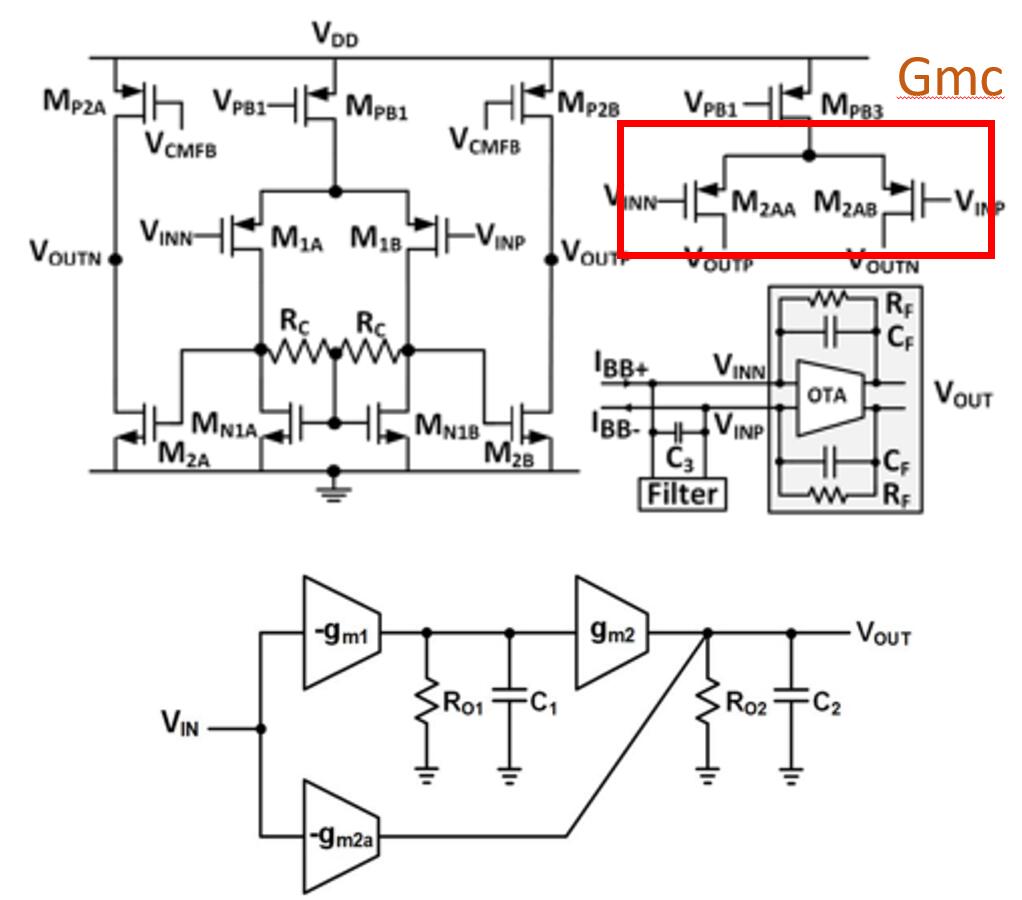
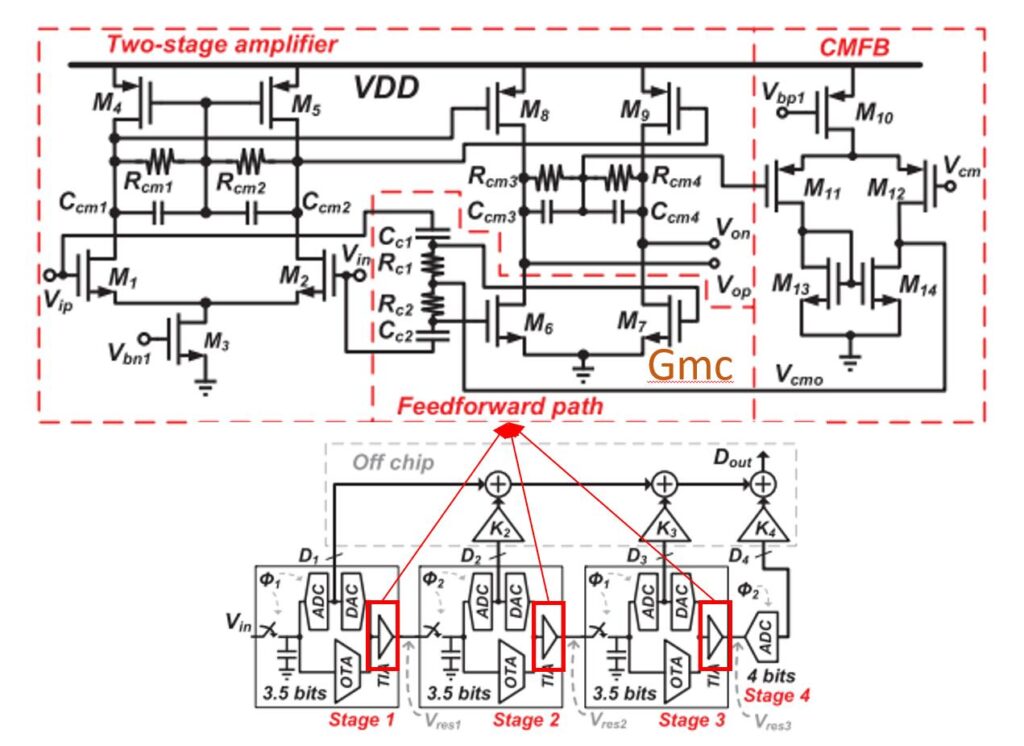
2019年，Junning Jiang 等人使用两级前馈补偿结构的运放设计了一个用于超宽带接收机模拟基带中的 TIA 电路。该电路中所用的运放结构如图3-2 所示^[1]。该运放使用了一个单独的 Gm2 级进行前馈补偿，最终在 18 mW 的功耗下实现了 39.4 dB 的直流增益、1.1 GHz 的增益带宽积。同时使用该运放设计的 TIA 电路的带宽达到了 200 MHz。

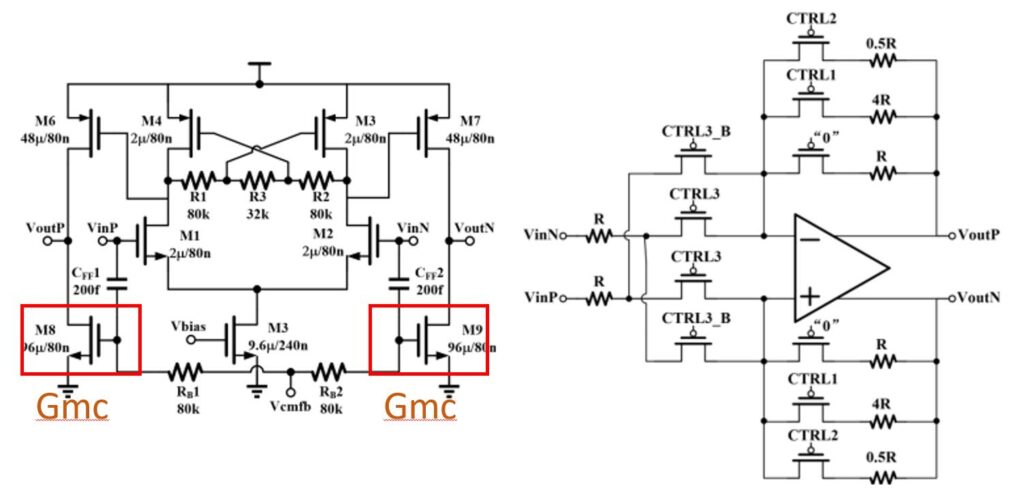
Dadian Zhou 等人同样使用两级前馈补偿结构的运放设计了一个用于 Plpline ADC 的级间放大的宽带运算放大器，其电路结构如图 3-3 所示^[2]。该运放利用了 Gm2 级空闲的 MOS 晶体管作为前馈补偿晶体管使用，节省了大量的功耗。该运放在 1.8 mA 的电流下实现了 6.2 GHz 的增益带宽积，同时实现了 41 dB 的增益以及 70 度的相位裕度。

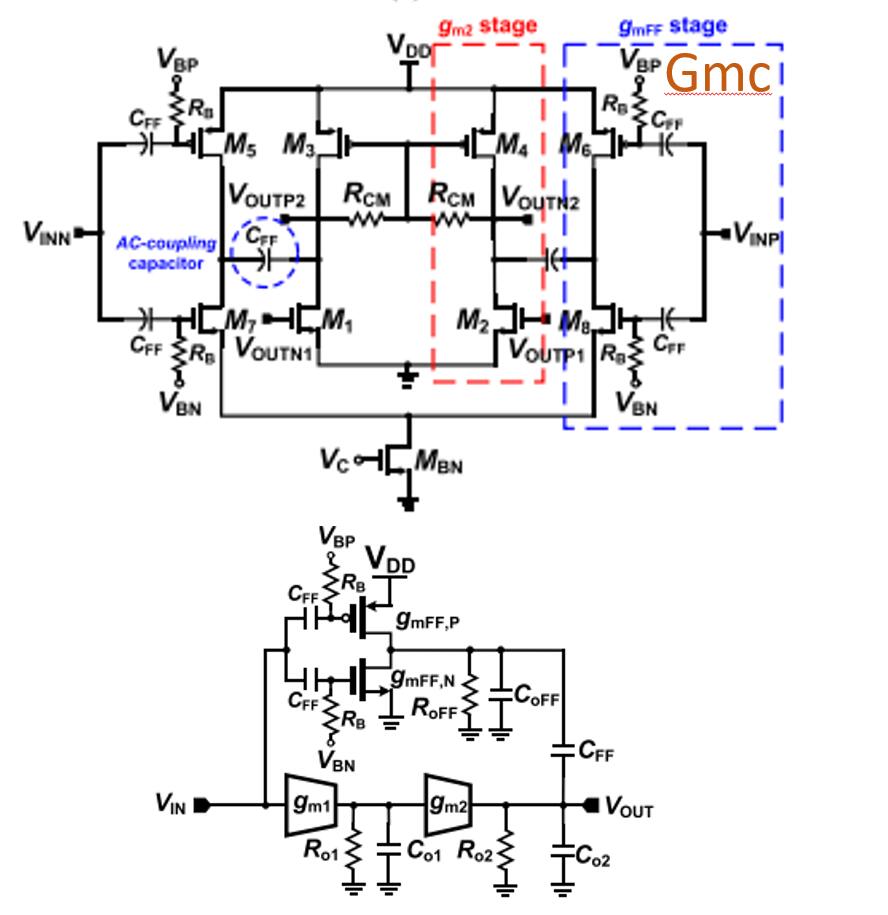
2020 年，Hyunki Jung 等人使用两级前馈补偿结构的运放设计了一个用于接收机 TIA 电路的运放，其结构如图3-4所示^[3]。该运放同时使用了一个 NMOS 和一个 PMOS 进行前馈补偿，在只消耗一路功耗的情况下实现了跨导的提升。该运放实现了 5 GHz 的增益带宽积以及 50 dB 的增益，以及 26.8 dBm 的带内 IIP3，同时整个 TIA 的功耗仅为 14.2 mW。

Jian Shao 等人两级前馈补偿结构的运放设计了一个用于接收机的可编程放大器电路的运放，其结构如图3-5所示^[4]。该运放同样将 Gm2 支路的晶体管进行复用，从而节省了两条支路的功耗。最终该运放在 2.02 mW 的功耗下实现了 1.7 GHz 的 GBW，42 dB 的增益以及 85 度的相位裕度。

5 总结

Gm 前馈补偿型运放能够在消耗较小的功耗的情况下实现一个较高的 GBW，在如今的超宽带和低功耗电路中的得到了广泛的应用。本文对 Gm 前馈补偿型运放进行了原理介绍，同时对前馈补偿型运放电路的应用进行了调研工作。理论分析显示在同样的功耗消耗情况下，相比于密勒补偿运放，前馈补偿运放的单位增益带宽可以实现 3~5 倍的提高。同时相对于单级放大器，两级密勒补偿运放的低频增益可以实现 20dB 的提高。